Inference, do you know it?
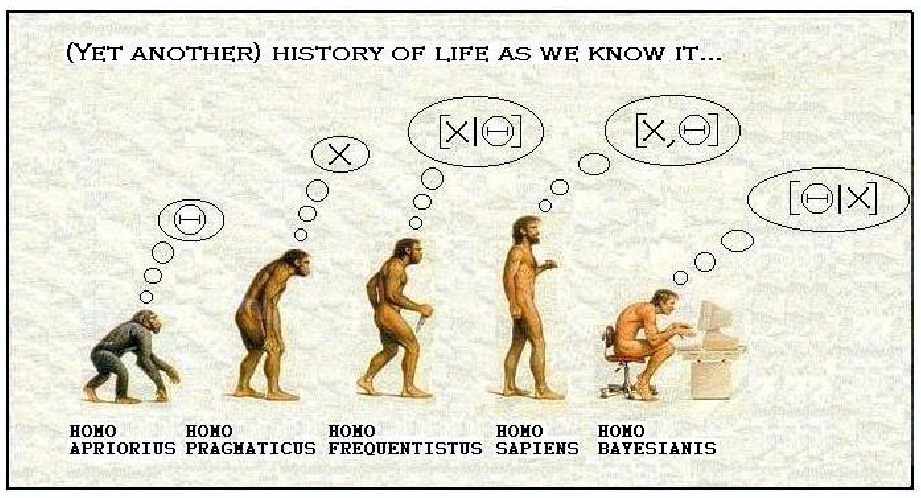
Image credit: from a talk
of Mike West
Figure legend (by me):
The Homo apriorius establishes the probability of an hypothesis, no matter
what data tell.
Astronomical example: H0=25. What the
data tell is uninteresting.
The Homo pragamiticus establishes that it is interested by the data only.
Astronomical example: In my experiment I found H0=66.6666666,
full stop.
The Homo frequentistus measures the probability of the data given the hypothesis.
Astronomical example: if H0=66.666666,
then the probability to get an observed value more different from the one
I observed is given by an opportune expression. Don't
ask me if my observed value is near the true one, I can only tell you that
if my observed values is the true one, then the probability of observing
data more extreme than mine is given by an opportune expression.
The Homo sapients measures the probability of the data and of the hypothesis.
Astronomical example: [missing]
The Homo bayesianis measures the probability of the hypothesis, given the
data.
Astronomical example: the true value of H0
is near 72 with +-3 uncertainty.
Give a look to my Bayesian primer for astronomers
The frequentist approach (i.e. the non-Bayesian one) prohibits to talk
about the error on the true value of a quantity because the true value is
a constant, and cannot fluctuate. Luis
Lyon 2002 used the word "Anathema" for frequentist statiscians talking
about error of a true value. Nevertheless, H0=72+-2 is read by
"most of us ... as saying that the constant is near 72, with 3 as some sort
of measurement of the uncertainty. If Bayesian methods are used, this is
indeed the correct interpretation ... However, if orthodox frequentist methods
have been used to derive these results, they must be interpreted differently:
here they would mean that if the actual value of H0 were
72, in some ensemble of repeated experiments [...] some given fraction (68%
or 95%, for example) of the results would lie in this range" (Andrew Jaffe, Science
301, 1329 (2003)). The frequentist paradigm provides a method
to construct intervals that, in the long run, have the property of including
the true value with the stated frequency, nothing less nothing more.
It may say nothing about the degree of accuracy with wich the quantity is
measured, but it say a lot about the method used to build the confidence
interval. Consider, for example the following valid confidence interval:
take a random number from 0 to 1 (uniformly distributed). If x<=0.68 is
found, then the 68 % confidence interval for your measure is the whole real
axis. If x>0.68, the 68 % confidence interval is empty. Does such a valid
confidence interval measure the uncertainty of the measure? An implementation of the above idea is here.
If you question the validity of the above confidence interval, let now
consider the standard confidence interval and the following case: the observed
background plus signal is smaller than the expected background alone (e.g.
Kraft
et al. 1991, ApJ, 374, 344 for an astronomical worked out example,
and ... for an high energy particle example). For example, you expected to
observe 5 background events, but only 3 (signal+background) have been recorded.
There is nothing unusual in that, because the background can fluctuate. In
such a case, the 68 % confidence interval has zero lenght. Does this mean
that the measure of the signal is extreamly accurate (what is shorter than
a zero lengh interval?), and cannot be improved, for example in a much expensive
experiment with a lower background?
Let now consider any other confidence interval, at the reader choice. The
frequentist paradigm provides an interval with the stated coverage. For example,
in the long run 68 % of the 68 % confidence intervals includes the true value.
Does this means that the true value has a 68 % probability to be inside the
68 % confidence interval ? No, it doesn't, and it is not a word game. Instead
of start to be tedious with the Bayes theorem (that states precisely that),
let consider the much simpler example: there is a 3 % probability that a
woman is pregnant. Does it means pregnant peoples have a 3 % probability
to be woman? (example taken from Luis
Lyon, 2002, where you also find explained the other famous example of
the dog and the hunter, due to D'Agostini). If x
% of the intervals cover the true value, this does not implyes that the
true value is included in a given interval with x % probability!
If you think that, most of the times, pregnant peoples are women, you agree
with I.J. Good: "All animals, including non-Bayesian statiscians,
are informal Bayesian" (in The Bayes/Non-Bayes compromise: a brief review,
J. Amer. Statist. Assoc. 87, 597 (1992), cited by Luc Demortier (2004)),
because you refuse the swapping above (called frequentist twist by Roger Barlow in Statistics for HEP).
To conclude, confidence contours are not measures of the uncertainty of
the measured quantity, unless they (numerically) coincide with credible (Bayesian)
intervals.
Useful links:
D'Agostini pages:
and his lanl talk
Bayesian primer di Luis
Lyon, 2002
CDF
Asymetric errors
look at this
list too
Durham
2002 workshop
Jim
Linnemann links
